Code examples
Bitwise Logical Operators
Bitwise AND
The bitwise AND operator (&) performs logical conjunction on the corresponding bits of its operands. For each pair of bits occupying the same position in the two numbers, it returns a one only when both bits are switched on:
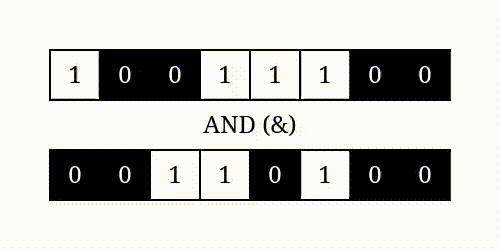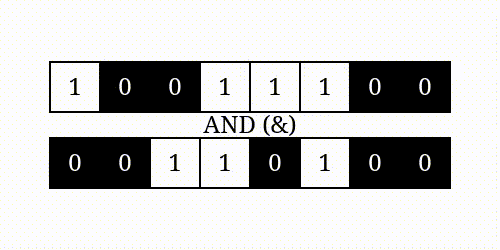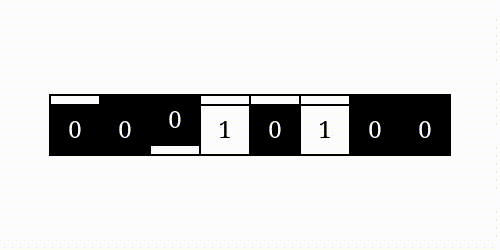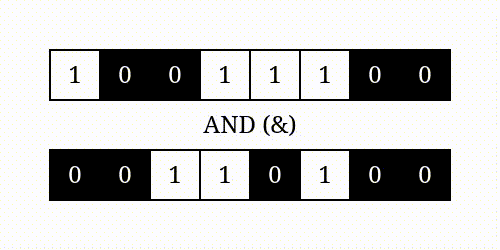
The resulting bit pattern is an intersection of the operator’s arguments. It has two bits turned on in the positions where both operands are ones. In all other places, at least one of the inputs has a zero bit.
Arithmetically, this is equivalent to a product of two bit values. You can calculate the bitwise AND of numbers a and b by multiplying their bits at every index i:
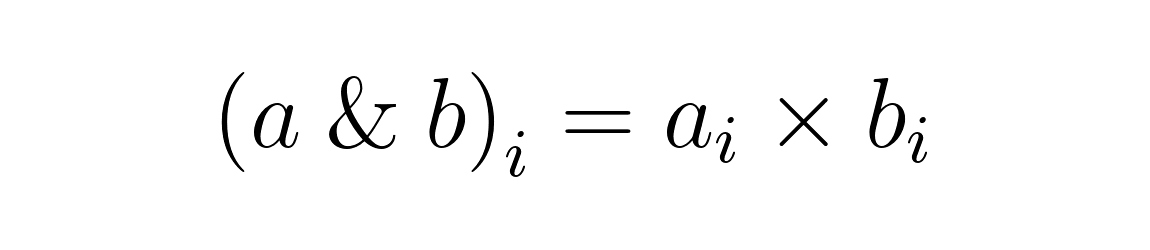
Here’s a concrete example:
| Expression | Binary Value | Decimal Value |
|---|---|---|
a | 100111002 | 15610 |
b | 1101002 | 5210 |
a & b | 101002 | 2010 |
A one multiplied by one gives one, but anything multiplied by zero will always result in zero. Alternatively, you can take the minimum of the two bits in each pair. Notice that when operands have unequal bit-lengths, the shorter one is automatically padded with zeros to the left.
Bitwise OR
The bitwise OR operator (|) performs logical disjunction. For each corresponding pair of bits, it returns a one if at least one of them is switched on:
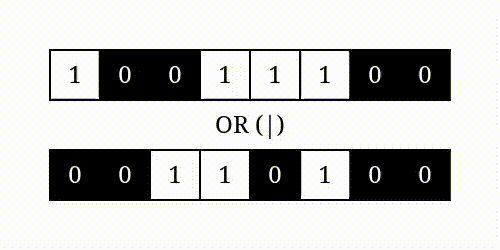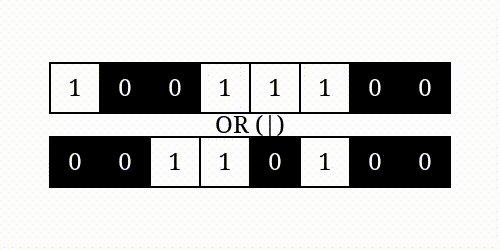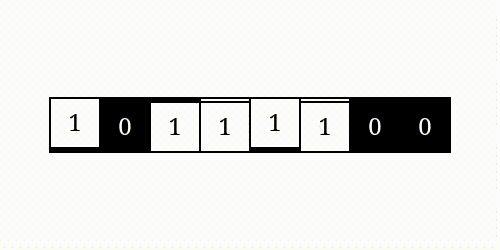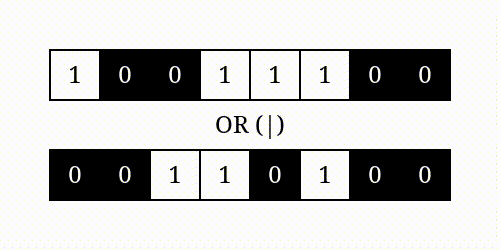
The resulting bit pattern is a union of the operator’s arguments. It has five bits turned on where either of the operands has a one. Only a combination of two zeros gives a zero in the final output.
The arithmetic behind it is a combination of a sum and a product of the bit values. To calculate the bitwise OR of numbers a and b, you need to apply the following formula to their bits at every index i:
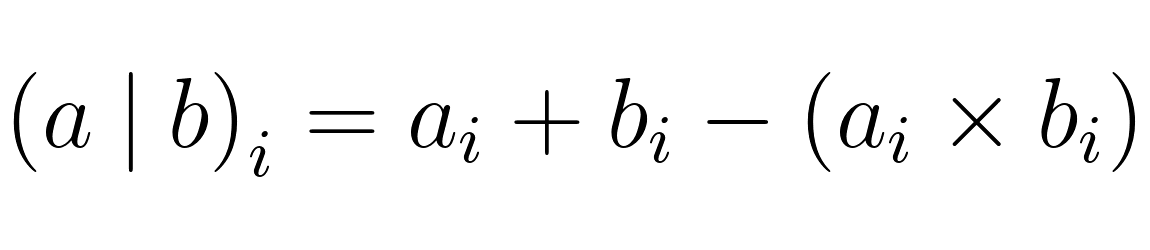
Here’s a tangible example:
| Expression | Binary Value | Decimal Value |
|---|---|---|
a | 100111002 | 15610 |
b | 1101002 | 5210 |
a | b | 101111002 | 18810 |
It’s almost like a sum of two bits but clamped at the higher end so that it never exceeds the value of one. You could also take the maximum of the two bits in each pair to get the same result.
Bitwise XOR
It evaluates two mutually exclusive conditions and tells you whether exactly one of them is met. For example, a person can be either a minor or an adult, but not both at the same time. Conversely, it’s not possible for a person to be neither a minor nor an adult. The choice is mandatory.
The name XOR stands for “exclusive or” since it performs exclusive disjunction on the bit pairs. In other words, every bit pair must contain opposing bit values to produce a one:
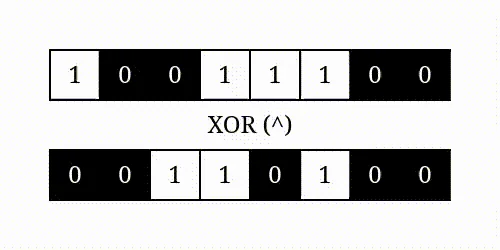
Visually, it’s a symmetric difference of the operator’s arguments. There are three bits switched on in the result where both numbers have different bit values. Bits in the remaining positions cancel out because they’re the same.
Similarly to the bitwise OR operator, the arithmetic of XOR involves a sum. However, while the bitwise OR clamps values at one, the XOR operator wraps them around with a sum modulo two:
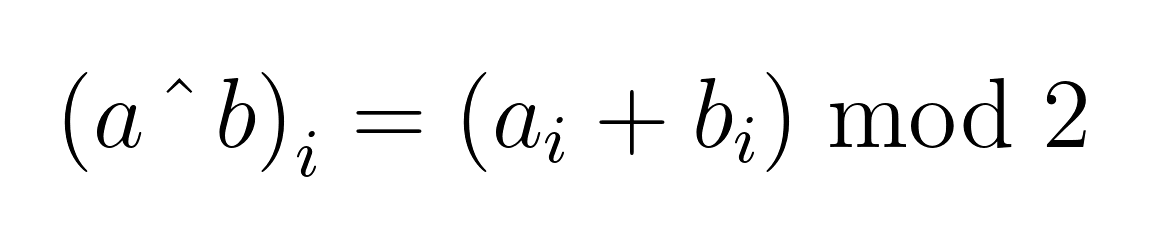Modulo is a function of two numbers—the dividend and the divisor—that performs a division and returns its remainder. In Python, there’s a built-in modulo operator denoted with the percent sign (%).
Once again, you can confirm the formula by looking at an example:
| Expression | Binary Value | Decimal Value |
|---|---|---|
a | 100111002 | 15610 |
b | 1101002 | 5210 |
a ^ b | 101010002 | 16810 |
The sum of two zeros or two ones yields a whole number when divided by two, so the result has a remainder of zero. However, when you divide the sum of two different bit values by two, you get a fraction with a remainder of one. A more straightforward formula for the XOR operator is the difference between the maximum and the minimum of both bits in each pair.
Bitwise NOT
The last of the bitwise logical operators is the bitwise NOT operator (~), which expects just one argument, making it the only unary bitwise operator. It performs logical negation on a given number by flipping all of its bits:
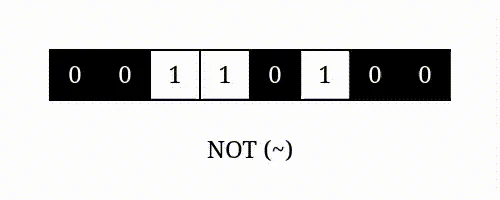
The inverted bits are a complement to one, which turns zeros into ones and ones into zeros. It can be expressed arithmetically as the subtraction of individual bit values from one:
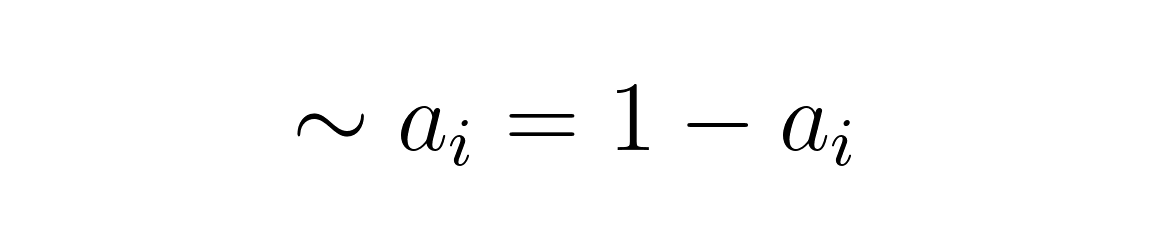
Here’s an example showing one of the numbers used before:
| Expression | Binary Value | Decimal Value |
|---|---|---|
a | 100111002 | 15610 |
~a | 11000112 | 9910 |
Tip
While the bitwise NOT operator seems to be the most straightforward of them all, you need to exercise extreme caution when using it in Python. Everything you’ve read so far is based on the assumption that numbers are represented with unsigned integers.
Although there are ways to simulate unsigned integers, Python doesn’t support them natively. That means all numbers have an implicit sign attached to them whether you specify one or not. This shows when you do a bitwise NOT of any number:
>>> ~156 -157
Instead of the expected 99, you get a negative value! The reason for this will become clear once you learn about the various binary number representations. For now, the quick-fix solution is to take advantage of the bitwise AND operator:
>>> ~156 & 255 99
Bitwise Shift Operators
Bitwise shift operators are another kind of tool for bit manipulation. They let you move the bits around, which will be handy for creating bitmasks later on. In the past, they were often used to improve the speed of certain mathematical operations.
Left Shift
The bitwise left shift operator (<<) moves the bits of its first operand to the left by the number of places specified in its second operand. It also takes care of inserting enough zero bits to fill the gap that arises on the right edge of the new bit pattern.
Right Shift
The bitwise right shift operator (>>) is analogous to the left one, but instead of moving bits to the left, it pushes them to the right by the specified number of places. The rightmost bits always get dropped.
References
📂 Computer Science | Последнее изменение: 05.03.2024 20:11